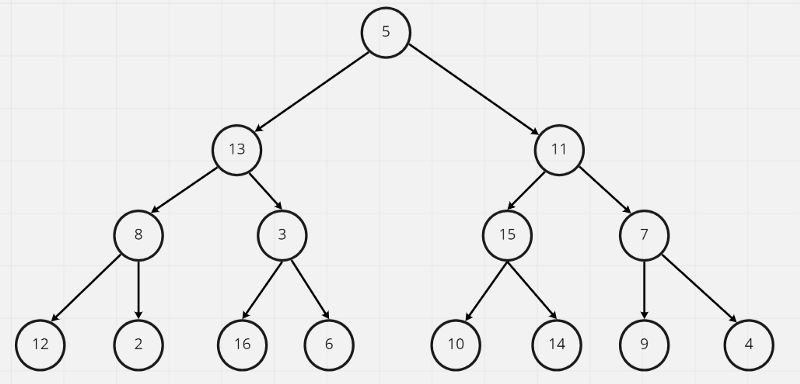
heap sort的原理是採用max heap這種資料結構來做排序，max heap是一種binary tree，每個節點都會比自己的子節點還大，因此根節點會是最大值，讓我們先來理解如何實作一個max heap吧!假設現在有一個排序是亂的binary tree如下圖

1. 先從右邊的subtree開始，如果subtree的父節點不是最大值就跟子節點做交換，7跟9交換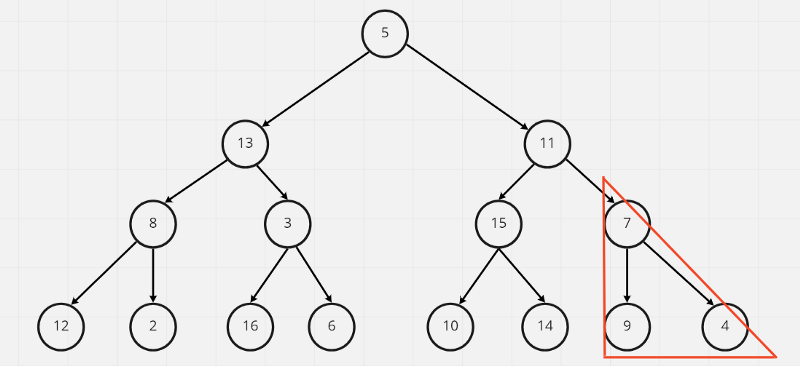
   
   紅色圈起來的就是subtee(子樹)

2. 15已是最大值，所以不用跟子節點交換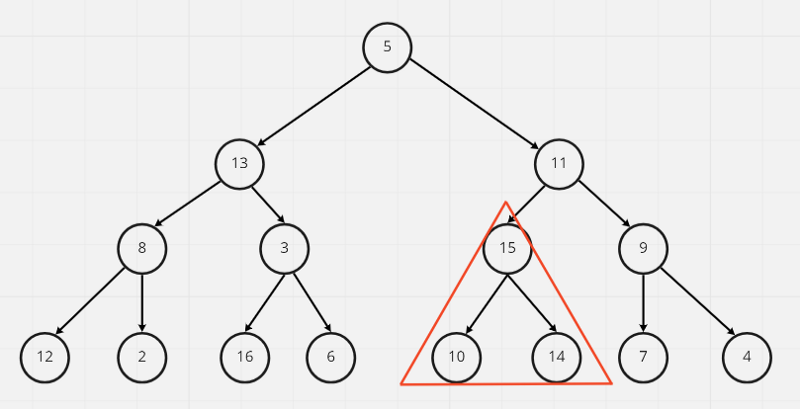
   

3. 16為最大值，故與3做交換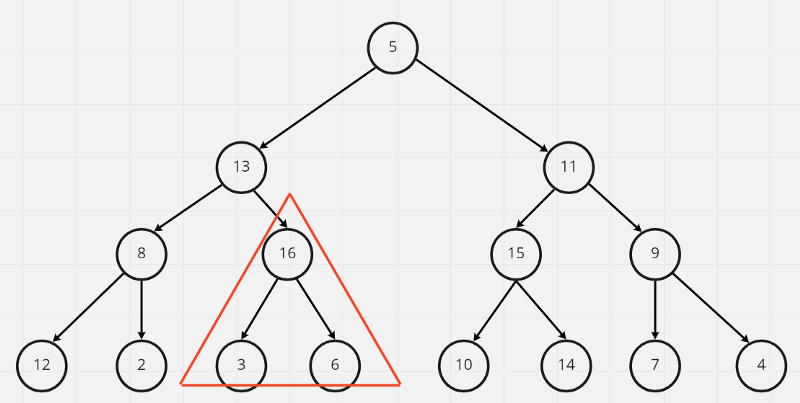
   

4. 12與8做交換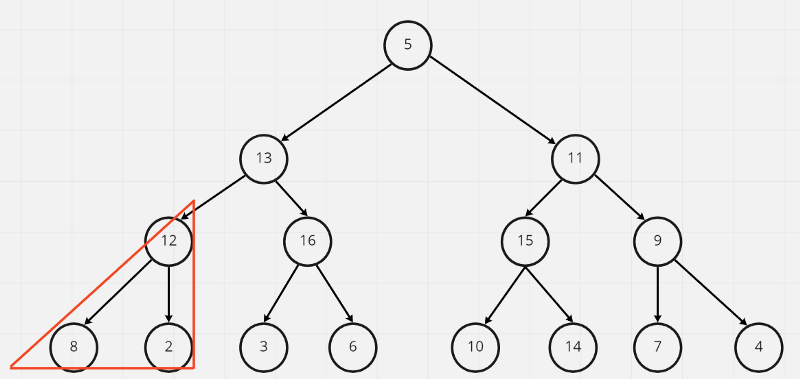
   

5. 當最下層的節點都遍歷完了，就輪到上面一層，15與11交換，不過這時候會發現一個問題，交換過後11, 10 ,14這個subTree並不是一個max heap，因此還要再做一次交換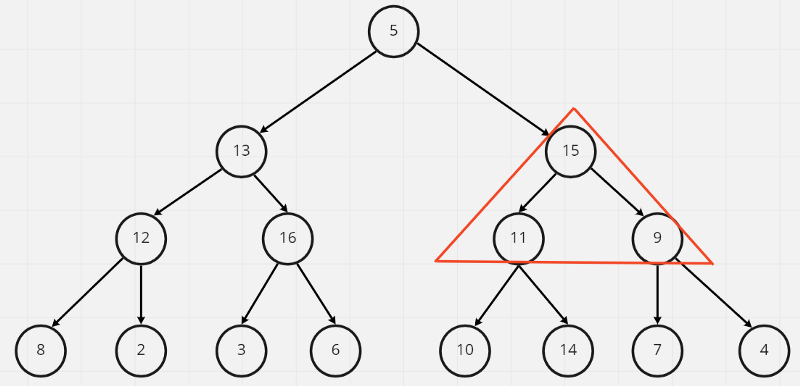
   

6. 因此14與11交換，每次交換的時候都要檢查下一層的值是否有比當前的值還大，有的話當前值就要跟較大值對調位置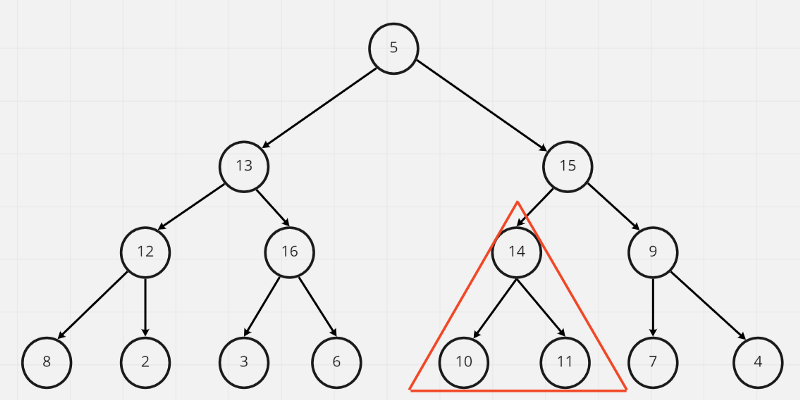
   

這樣依序的交換過一輪最後就會獲得一個max-heap!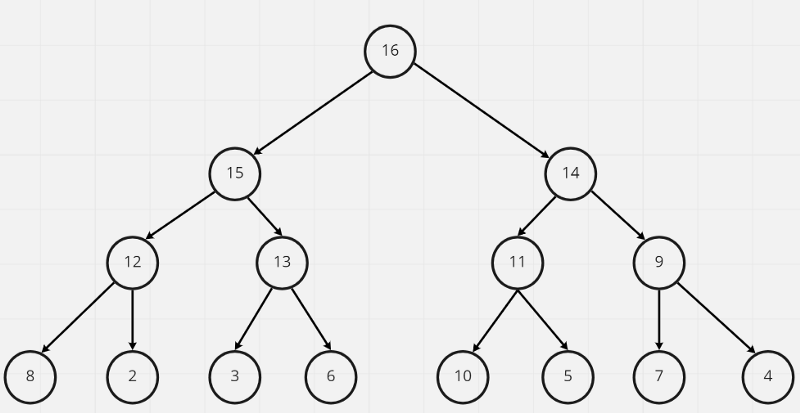

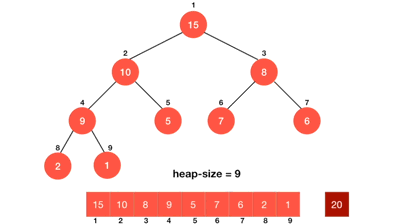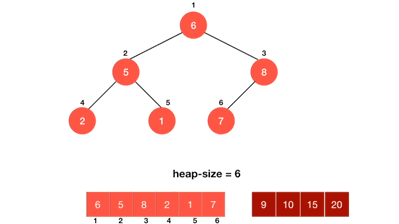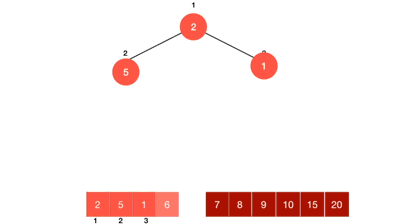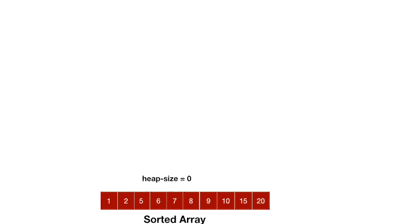
理解了max-heap的運作原理之後，就可以來探討如何用max-heap做heap sort了。

1. 先將根節點(16)與leaf node最右邊的節點(4)做交換，此時4會在根節點的位置，16會跑到右下角，接著移除右下角的節點並取出16放在下方，這時會發現4並不是這整顆樹裏面的最大值，因此4要向下交換

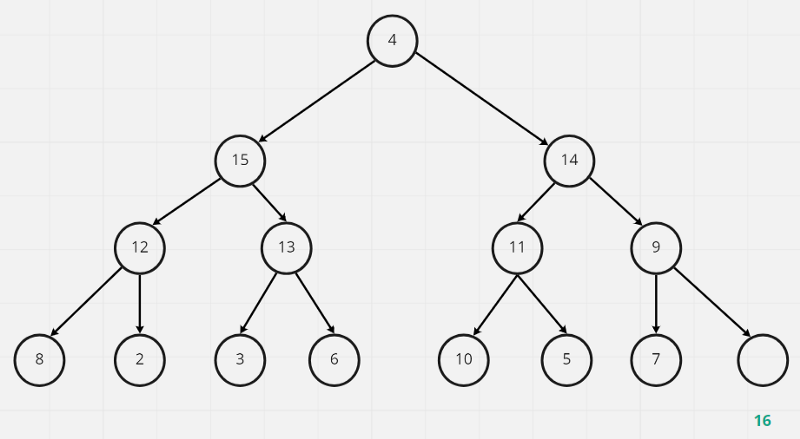
綠色的數字為取出的數字

2. 交換過後如果發現下面還有比自己更大的值就要一直交換下去，最後4來到了這個位置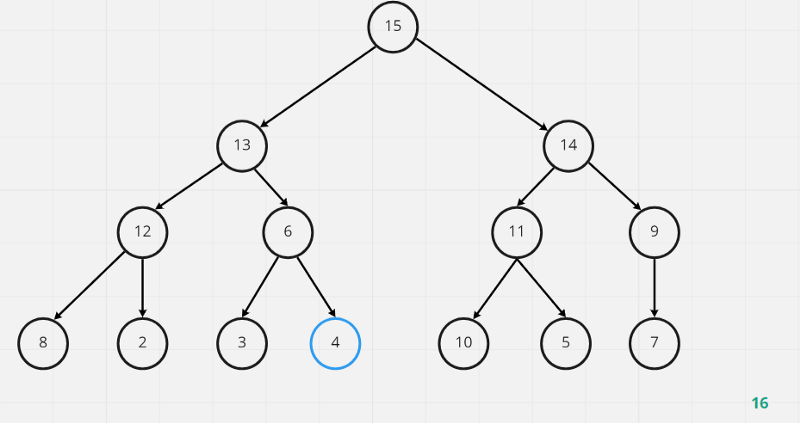
   
   經過一輪交換，最後4停留在這個位置

3. 這時會發現15已經是整個max-heap的最大值，於是跟leaf node下層最右邊的節點7做交換，再把15從節點中抽離出來，接下來就是一直不斷的重複這個動作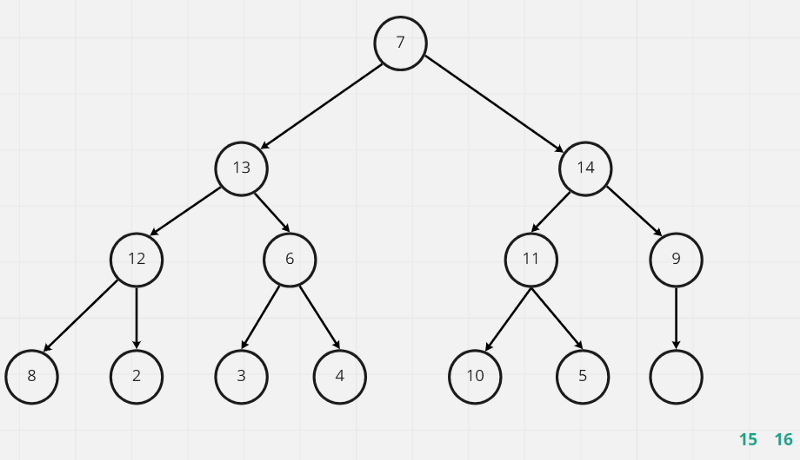
   

如果還是覺得有點抽象的話，可以參考heap sort的流程的gif，應該可以幫助理解，畫面中的heapify指的是將根節點一路向下交換的過程

圖片來源:Cakeresume.com

用js實作max heap

首先先將tree轉換成陣列，由上到下將每個節點取出的話 ，可以得到一個陣列[5, 13, 11, 8, 3, 15, 7, 12, 2, 16, 6, 10, 14, 9, 4]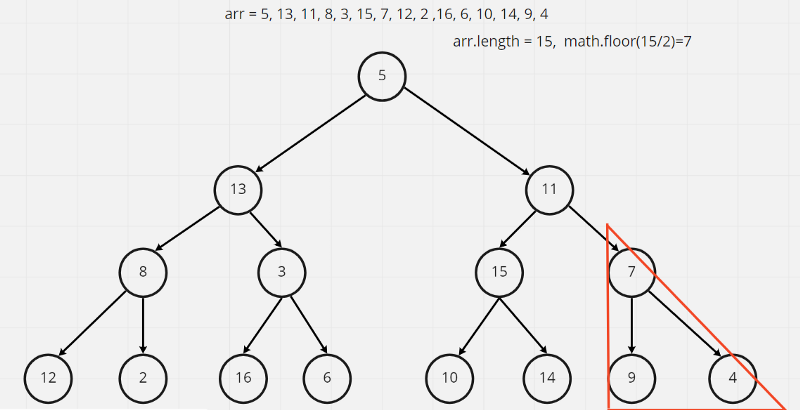

1. 需要先建立一個maxHeap，透過起始點的公式(Math.floor(heapSize / 2))算出7，先從index 7 (數字12)開始，但因為12沒有子節點，所以往index 6移動(數字7)，開始執行heapify
2. 經過不斷的heapify，最大值會移動到根節點
3. 根節點與left node最右邊的節點做交換，將最大值取出，移除left node最右邊的節點
4. 此時根節點並非最大值，需要再次進行步驟2，不斷重複…
5. 直到全部節點都取出，陣列就排序完成了

用js實作heap sort

const createMaxheap = (arr, heapSize) => {
    //從 Math.floor(heapSize / 2)這個節點開始檢查
    for (let i = Math.floor(heapSize / 2); i >= 0; i--) {
        maxHeapify(arr, i, heapSize);
    }
};
const maxHeapify = (arr, i, heapSize) => {
    let largest;
    let left = i * 2 + 1; //取自己的左子節點
    let right = i * 2 + 2; //取自己的右子節點
    //檢查subtree裡面 誰是最大值?
    largest = left <= heapSize && arr[left] > arr[i] ? left : i;
    if (right <= heapSize && arr[right] > arr[largest]) {
        largest = right;
    }

    //如果subtree的parent不是最大的 就持續向下交換
    if (largest != i) {
        [arr[i], arr[largest]] = [arr[largest], arr[i]];
        maxHeapify(arr, largest, heapSize);
    }
};

const heapSort = (arr) => {
    let heapSize = arr.length - 1;
    //先建立maxHeap
    createMaxheap(arr, heapSize);
    for (let i = arr.length - 1; i >= 0; i--) {
        //將leaf node最右邊那個跟根節點交換
        [arr[0], arr[i]] = [arr[i], arr[0]];
        //節點取出後 heapSize-1
        heapSize -= 1;
        //此時根節點並非最大值 需要執行maxHeapify
        maxHeapify(arr, 0, heapSize);
    }
    return arr;
};

heapSort([5, 13, 11, 8, 3, 15, 7, 12, 2, 16, 6, 10, 14, 9, 4]);

不得不說 heap sort是我覺得最難理解的排序演算法 ，需要反覆消化很多次才能理解

時間複雜度

• 在最差的情況下，時間複雜度是O(n log n)
• 在最佳的情況下，時間複雜度是O(n log n)
• 在平均情況下，時間複雜度為 O(n log n)